
Gestión de la programación de tareas para producción en talleres de maquinado con sistemas MOEAs
MSc. Hiovanis Castillo Pantoja
Universidad de Holguín
ORCID: 0000-0003-0091-0904
hiovanisc@uho.edu.cu
Dr.C. Lidia María Pérez Vallejo
Universidad de Holguín
ORCID: 0000-0001-8602-5898
lidia@uho.edu.cu
Dr.C. Roberto Pérez Rodríguez
Universidad de Holguín
ORCID: 0000-0001-5741-5168
roberto.perez@uho.edu.cu
RESUMEN
En la actualidad, la gestión de la programación productiva en las empresas de manufactura determina el uso eficiente de los recursos y la entrega a tiempo de los productos terminados a los clientes. En este contexto, ante las limitaciones en la logística de las materias primas las plantas industriales adoptan soluciones basadas en la optimización multi-objetivo para la gestión de las capacidades de producción. Este trabajo se enfoca en la mejora de la eficiencia de las producciones a corto plazo en talleres de maquinado, empleando la variante del método evolutivo multi-objetivo (MOEAs). Se consideran en el modelo óptimo multi-objetivo tres variables: costo de producción, volumen de producción y el acabado superficial de las piezas. Se toman cuatro objetivos a minimizar: velocidad de la herramienta circular abrasiva, velocidad de la pieza, profundidad de corte y avance. Como caso de estudio se tomó un proceso de rectificado para la producción de piezas metálicas prismáticas en un taller de maquinado. Se muestra la evaluación cuantitativa de la gestión de la programación de la producción y se demuestra la efectividad del método propuesto al realizar la comparación con dos métodos de optimización.
Palabras clave: Gestión, programación de tareas, MOEAs, NSAG-III, maquinado.
Management of task scheduling for production in machining workshops with MOEAs systems
ABSTRACT
Currently, the management of productive programming in manufacturing companies determines the efficient use of resources and the timely delivery of finished products to customers. In this context, given the limitations in the logistics of raw materials, industrial plants adopt solutions based on multi-objective optimization for the management of production capacities. This work focuses on improving the efficiency of short-term production in working shops, using the variant of the multi-objective evolutionary method (MOEAs). Three variables are considered in the optimal multi-objective model: production cost, production volume and the surface finish of the parts. Four objectives are taken to minimize: speed of the abrasive tool, speed of the part, depth of cut and feed. As a case study, a grinding process was taken for the production of prismatic metal parts in a working shop. The quantitative evaluation of the management of the production schedule is shown and the effectiveness of the proposed method is demonstrated when making the comparison with two optimization methods.
Keywords: Management, scheduling, MOEAs, NSAG-III, machining.
INTRODUCCIÓN
Los algoritmos evolutivos multiobjetivo (AEMO) se han utilizado ampliamente para operar problemas complejos de ingeniería en las últimas décadas. Esto se debe a que es difícil obtener soluciones óptimas para problemas complejos utilizando técnicas de optimización tradicionales, como la programación no lineal (Huang et al., 2017). Con este fin, se ha estimulado el desarrollo y aplicación de los AEMO para resolver los complejos problemas de optimización de la planificación y gestión de los recursos con múltiples objetivos de diseño y operación (Fu et al., 2013).
Hasta el momento, los AEMO se han utilizado para resolver problemas en la industria de la manufactura con el objetivo de alcanzar estándares de calidad en el acabado superficial de las piezas. El proceso de rectificado es uno de los métodos más utilizados para alcanzar este objetivo. Por tanto, es necesario la mejora de la gestión de los parámetros principales del proceso de rectificado, incorporándole métodos modernos de optimización para la toma de decisiones que se corresponden con el aumento de las producciones y el ahorro de recursos materiales y energéticos. (Patil, et al., 2019) desarrollan un modelo matemático utilizando la metodología de superficie de respuesta (RSM). Los resultados de RSM se utilizan, además, para obtener soluciones óptimas de frente de Pareto utilizando el enfoque NSGA-II.
Por su parte, (Fu et al., 2013) utilizan un algoritmo evolutivo multiobjetivo denominado algoritmo genético ordenado no dominado (NSGA-II) y análisis visuales interactivos para revelar y explorar las ventajas y desventajas del problema de una red. Este trabajo demuestra que un enfoque de análisis visual de diversos objetivos tiene claras ventajas y beneficios para respaldar una toma de decisiones más informada y transparente en el proceso de diseño.
(Huang et al., 2017) realizan un análisis probabilístico basado en la simulación de Monte-Carlo y en el análisis de sensibilidad global para la evaluación previa de los efectos de la demanda nodal transitoria. Los resultados y el análisis de la aplicación confirman la eficacia y la mejora del método desarrollado en este estudio sobre la orientación del modelado y análisis transitorios precisos bajo la influencia de las demandas nodales. Proponen la combinación del algoritmo HMOMA y NSGA-III, para ampliar el conjunto de soluciones basadas en ajustes colaborativos de procesos y equipos.
(Wang et al., 2019) desarrollan un modelo de optimización de varios objetivos para planificar la aplicación de los cuatro tipos de variables de decisión: equipos de proceso, tecnologías de producción más limpia, tecnologías de tratamiento al final del proceso y tecnologías sinérgicas. Además, para formular esquemas de decisión final, adoptan el algoritmo de agrupamiento Fuzzy C-means para agrupar las soluciones óptimas de Pareto. Los resultados muestran que NSGA-III se desempeña bien en la distancia entre centros, la métrica de espaciado y la eficiencia computacional. Se demuestra que la metodología propuesta es capaz de resolver problemas de optimización multiobjetivo y ayudar a la toma de decisiones en la gestión ambiental industrial.
El rectificado es uno de los procesos de mecanizado de precisión que consumen más energía. La eficiencia energética no se ha considerado completamente en las estrategias de rectificado tradicional para obtener beneficios en la producción. Por lo tanto, (Wang, et al., 2021) proponen un método de diseño óptimo para obtener parámetros de rectificado considerando la gestión de energía y el rendimiento de mecanizado. Se desarrolló un modelo no paramétrico basado en la red neutra artificial adaptativa mejorada (aANN) para predecir la calidad de la superficie, el tiempo de mecanizado y el consumo de energía total. Los resultados experimentales en el acero AISI 1045 demostraron que la solución óptima podría mejorar la eficiencia energética en un 89,52 % y reducir el tiempo de mecanizado en un 174,36 % manteniendo la misma calidad del producto.
En otro estudio, (Xi et al., 2021) establece un modelo de mantenimiento selectivo de tres objetivos para el sistema serie-paralelo para minimizar el costo de mantenimiento, maximizar la probabilidad de completar la siguiente tarea y minimizar el tiempo de inactividad. El modelo de toma de decisiones de mantenimiento y el modelo de asignación de personal se combinan para tomar decisiones sobre la duración óptima del período de descanso de cada equipo, el equipo que se mantendrá durante el período de descanso y el nivel de mantenimiento. Para el modelo multiobjetivo establecido, se diseña el algoritmo NSGA-III. Comparando con el algoritmo NSGA-II que solo considera los dos primeros objetivos, se verifica que el modelo multiobjetivo diseñado puede reducir efectivamente el tiempo de inactividad del sistema.
En otro análisis, (Sang et al., 2022) proponen un algoritmo memético de varios objetivos de alta dimensión (HMOMA). Este método combina la NSGA-III mejorada y el método de búsqueda local. Para expandir efectivamente el espacio del conjunto de soluciones, se diseña la estructura de vecindario basada en el ajuste colaborativo de procesos y equipos y en la ruta crítica. Para mejorar el rendimiento integral de la población, se propone un método de selección de entorno de modo dual. La viabilidad y competitividad del modelo de programación y HMOMA se verifican mediante experimentos. La solución de este problema tiene un significado académico importante y un valor de ingeniería para la fábrica inteligente.
Se observa en la revisión bibliográfica la necesidad de desarrollar métodos combinados que aprovechen las ventajas de la optimización multiobjetivo para la gestión de los procesos de mecanizado con más de dos criterios. Por tanto, el objetivo de este trabajo es mostrar la aplicación de las herramientas AEMO representado con el algoritmo NSAG-III, como modelos de optimización multiobjetivo. Se presentan los resultados preliminares aplicados a un caso de estudio.
METODOLOGÍA
En general, el problema de optimización puede expresarse mediante el siguiente modelo matemático:
![]() (1)
(1)
![]()
![]() (2)
(2)
![]() (3)
(3)
Donde m y l son el número de restricciones de
desigualdad e igualdad, respectivamente. En primer lugar, se describirán las condiciones
necesarias que debe satisfacer una solución óptima. Sea ![]() la función a
minimizar, con las funciones de restricción
la función a
minimizar, con las funciones de restricción ![]() y
y ![]() . Supongamos
que estas funciones son continuamente diferenciables en el punto
. Supongamos
que estas funciones son continuamente diferenciables en el punto ![]() . Si
. Si ![]() es un mínimo
local, existen constantes
es un mínimo
local, existen constantes ![]() ,
, ![]() and
and ![]() , y tales
que:
, y tales
que:
![]() (4)
(4)
![]() (5)
(5)
Se muestran las condiciones suficientes que garantizan la existencia de un óptimo global. Si existen constantes y tales que:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Las condiciones suficientes son garantizadas y la existencia de un óptimo global son:
![]() ,
, ![]() convexo,
convexo, ![]() , y un punto
, y un punto ![]() . Si existe
la constante
. Si existe
la constante ![]() y
y ![]() entonces:
entonces:
![]() (9)
(9)
![]() (10)
(10)
El punto ![]() es el mínimo
global de
es el mínimo
global de ![]() , como se
constata en la literatura que ha sido establecida como referencia.
, como se
constata en la literatura que ha sido establecida como referencia.
Algoritmo NSAG-III
Los métodos de optimización evolutiva multiobjetivo (EMO) han demostrado ampliamente su eficacia para encontrar un conjunto de soluciones no dominadas, convergentes y diversificadas en diferentes problemas de optimización de dos y tres objetivos desde principios de los años 90 (Kahhal et al., 2013). Los autores proponen un nuevo método que utiliza el procedimiento basado en el algoritmo NSGA-II que trabaja con un conjunto de puntos de referencia predefinidos, y demuestran que pueden resolver problemas de optimización de 2 a 15 objetivos con una eficacia correcta. NSAG- III ha sido evaluado por varias pruebas experimentales con un rendimiento altamente competitivo.
El funcionamiento para el análisis multi objetivo considera los siguientes aspectos:
1. El problema de optimización multiobjetivo es un conjunto de soluciones óptimas de Pareto que sigue una distribución uniforme y tiene una buena conveniencia y extensión.
2. La diversidad se mantiene mediante un conjunto de direcciones de referencia.
3. La convergencia está garantizada por los puntos de referencia uniformemente distribuidos en el hiperplano.
4. Si existen varios miembros de la población asociados al punto de referencia, se selecciona el que tenga la mínima distancia perpendicular.
5. El punto de referencia se desprecia en la generación actual, cuando existe un miembro de la población asociado a él.
Modelo propuesto.
El modelo matemático tomado de (Zhang et al., 2014) para la optimización de los parámetros de rectificado analizados en este trabajo, se expresa para los tres funciones objetivos seleccionados:
a) Costo de producción (CT)
 (11)
(11)
b) Volumen de producción (WRP)
The production rate is represented by the workpiece removal parameter WRP (cubic millimeters per minute Newton.
![]() (12)
(12)
La velocidad de producción está representada por el parámetro de retirada de piezas.
c) Acabado superficial (TAVE)
![]() (13)
(13)
El acabado superficial de la pieza de trabajo se suele especificar para que esté dentro de un cierto valor Ra que está fuertemente influenciado por los parámetros de operación y los parámetros de reavivado del rectificdo. Para determinar el valor de Ra, partimos del espesor medio de viruta durante el rectificado TAVE, expresado en la ecuación siguiente.
![]() (14)
(14)
Restricciones
En cuanto a las restricciones, los valores mínimos y máximos considerados para las recomendaciones de los parámetros de mecanizado (Vs, Vw, Doc, L) son proporcionados por los fabricantes de las herramientas de corte en sus catálogos. Los objetivos anteriores están sujetos a:
1000 < Vs < 2.023 (m/min) (15)
10 < Vw < 22.7 (m/min) (16)
0.01 < Doc < 0.14 (mm) (17)
0.01 < L < 0.14 (mm/rev) (18)
Determinación de las variables subjetivas y optimización del modelo
En este estudio se analiza establecer la relación de las variables subjetivas con la rugosidad y el acabado superficial al realizar la operación de rectificado. Para la rugosidad superficial del proceso de rectificado se relacionan como variables subjetivas el coste y el volumen de producción, considerando que los valores de rugosidad superficial no superen los valores requeridos. El acabado superficial se asume como subjetivo, combinado con el coste de producción; con la condición de que el volumen de producción no supere los valores exigidos.
Tomando el análisis de optimización multiobjetivo del problema en relación al proceso de rectificado superficial formulado mediante el algoritmo de ordenamiento no dominado NSAG-III y las restricciones presentadas (Ap = 0.0505, Aw = 0.1, Ra ≤ 1.8), la combinación de los pesos (W1=0.5, W2=0.5, W3=0.5, W3=0); en la función objetivo se puede minimizar la relación entre los valores numéricos subjetivos y la normalización de estos, con la ecuación 9:
![]() (19)
(19)
La optimización de las funciones objetivo se realiza con el algoritmo de clasificación genética no denominado NSAG-III, que nos permite obtener un mejor rendimiento analizando tres funciones para los resultados buscados para el proceso de molienda. Para el análisis partimos de una población de 92 datos. Los datos numéricos de entrada se muestran en la Tabla 1 y los valores límite definidos para este trabajo se muestran en la Tabla 2.
Tabla 1.
Datos numéricos de entrada.
|
No. |
Code |
Value |
No. |
Code |
Value |
|
1 |
Mc |
30 $/h |
17 |
Nt |
12 |
|
2 |
P |
1 pc |
18 |
Ntd |
2000 pc |
|
3 |
Lw |
300 mm |
19 |
Cd |
25.00 $ |
|
4 |
Lc |
25 mm |
20 |
Cs |
0.003 $/mm3 |
|
5 |
fb |
2 mm/pass |
21 |
CT* |
10 $/pc |
|
6 |
aw |
0.1(r),0.055(f) mm |
22 |
Rc |
58 |
|
7 |
ap |
0.0505, 0.0105(f) mm/pass |
23 |
Ra* |
1.8 |
|
8 |
Sp |
2 pass |
24 |
VOL |
6.99% |
|
9 |
De |
355 mm |
25 |
dg |
0.3 mm |
|
10 |
bs |
25 mm |
26 |
WRP* |
20 mm3/minN |
|
11 |
G |
60 |
27 |
Km |
100 Nmm |
|
12 |
Sd |
100 mm |
28 |
Rem |
1 |
|
13 |
Vr |
254 mm/min |
29 |
A0 |
0 |
|
14 |
t1 |
5 min |
30 |
Ku |
3.937 x 10-7 mm-1 |
|
15 |
tch |
30 pc |
31 |
Ka |
0.0869 |
|
16 |
Nd |
20 |
|
|
|
Tabla 2.
Valores límites de las variables del proceso.
|
Vs(m/min) |
1.000-2.02 |
|
Vw(m/min) |
10.0-22.7 |
|
Doc (mm) |
0.01-0.14 |
|
L (mm/rev) |
0.01-0.14 |
RESULTADOS Y DISCUSION
La Tabla 3 muestra los resultados de convergencia del frente de Pareto al alcanzar 40 variantes, cuando se utilizan los algoritmos NSAG-III. El análisis de los tres objetivos utilizados (CT, WRP, TAVE) y la distribución de la dispersión de los puntos del frente de población se representa en la Figura. 1.
Tabla 3.
Resultados de convergencia para frente de pareto.
|
Idx |
f1=ct |
f2=WRP |
f3=Tave |
Vs |
Vw |
Doc |
COF |
Ra |
Tave(0.72) |
|
1 |
13.49 |
10.5 |
0.545 |
1.3 |
10 |
0.127 |
0.411 |
0.508 |
0.646 |
|
2 |
13.59 |
10.3 |
0.528 |
1 |
10 |
0.101 |
0.413 |
0.497 |
0.631 |
|
3 |
13.29 |
14 |
0.525 |
1.9 |
10 |
0.132 |
0.405 |
0.494 |
0.629 |
|
4 |
13.39 |
13 |
0.520 |
1.5 |
10 |
0.115 |
0.407 |
0.491 |
0.625 |
|
5 |
13.18 |
18 |
0.528 |
3.2 |
20 |
0.176 |
0.401 |
0.496 |
0.631 |
|
6 |
13.38 |
15.8 |
0.500 |
1.7 |
20 |
0.101 |
0.407 |
0.477 |
0.607 |
|
7 |
13.39 |
11.9 |
0.542 |
1.6 |
10 |
0.140 |
0.413 |
0.506 |
0.644 |
|
8 |
13.08 |
20.7 |
0.535 |
4.5 |
20 |
0.223 |
0.398 |
0.501 |
0.638 |
|
9 |
13.38 |
11.5 |
0.591 |
2.2 |
10 |
0.218 |
0.408 |
0.539 |
0.685 |
|
10 |
13.09 |
19.8 |
0.528 |
3.8 |
20 |
0.194 |
0.398 |
0.496 |
0.631 |
|
11 |
13.28 |
18.1 |
0.500 |
2.3 |
20 |
0.116 |
0.404 |
0.478 |
0.607 |
|
12 |
13.09 |
19.9 |
0.520 |
3.5 |
20 |
0.175 |
0.398 |
0.491 |
0.624 |
|
13 |
13.39 |
14 |
0.510 |
1.6 |
10 |
0.106 |
0.407 |
0.485 |
0.616 |
|
14 |
13.19 |
14.2 |
0.561 |
2.7 |
10 |
0.205 |
0.402 |
0.519 |
0.659 |
|
15 |
13.18 |
16.5 |
0.541 |
3.1 |
20 |
0.191 |
0.401 |
0.505 |
0.642 |
|
16 |
13.18 |
19.4 |
0.512 |
3.1 |
20 |
0.152 |
0.401 |
0.486 |
0.618 |
|
17 |
13.19 |
18.7 |
0.509 |
2.7 |
20 |
0.139 |
0.401 |
0.484 |
0.615 |
|
18 |
13.28 |
13.3 |
0.584 |
2.8 |
10 |
0.227 |
0.405 |
0.534 |
0.679 |
|
19 |
13.49 |
10.7 |
0.532 |
1.2 |
10 |
0.111 |
0.411 |
0.500 |
0.635 |
|
20 |
13.38 |
15.2 |
0.502 |
1.6 |
20 |
0.100 |
0.407 |
0.479 |
0.609 |
|
21 |
13.19 |
15 |
0.564 |
3.1 |
10 |
0.223 |
0.402 |
0.521 |
0.662 |
|
22 |
13.38 |
12.7 |
0.543 |
1.9 |
10 |
0.152 |
0.407 |
0.507 |
0.645 |
|
23 |
13.48 |
10.8 |
0.552 |
1.4 |
10 |
0.141 |
0.410 |
0.512 |
0.652 |
|
24 |
13.49 |
11.6 |
0.519 |
1.2 |
10 |
0.101 |
0.410 |
0.490 |
0.623 |
|
25 |
13.29 |
18.2 |
0.492 |
2 |
20 |
0.100 |
0.404 |
0.472 |
0.600 |
|
26 |
13.48 |
12.1 |
0.526 |
1.4 |
10 |
0.115 |
0.410 |
0.495 |
0.629 |
|
27 |
13.28 |
15.9 |
0.523 |
2.3 |
20 |
0.146 |
0.404 |
0.493 |
0.627 |
|
28 |
13.38 |
15.4 |
0.502 |
1.7 |
20 |
0.101 |
0.407 |
0.479 |
0.608 |
|
29 |
13.19 |
13.9 |
0.573 |
2.9 |
10 |
0.227 |
0.402 |
0.527 |
0.670 |
|
30 |
13.28 |
15.9 |
0.514 |
2.1 |
20 |
0.129 |
0.404 |
0.487 |
0.619 |
|
31 |
13.29 |
12.3 |
0.593 |
2.5 |
10 |
0.227 |
0.405 |
0.540 |
0.686 |
|
32 |
13.19 |
16.7 |
0.529 |
2.7 |
20 |
0.166 |
0.401 |
0.497 |
0.632 |
|
33 |
13.28 |
17.3 |
0.504 |
2.2 |
20 |
0.118 |
0.404 |
0.480 |
0.610 |
|
34 |
13.38 |
11.6 |
0.571 |
2 |
10 |
0.185 |
0.407 |
0.525 |
0.668 |
|
35 |
13.28 |
14.8 |
0.524 |
2.1 |
10 |
0.139 |
0.404 |
0.494 |
0.628 |
|
36 |
13.09 |
18 |
0.548 |
3.9 |
20 |
0.225 |
0.399 |
0.510 |
0.648 |
|
37 |
13.28 |
14.7 |
0.542 |
2.4 |
10 |
0.172 |
0.404 |
0.506 |
0.643 |
|
38 |
13.39 |
11.1 |
0.567 |
1.7 |
10 |
0.170 |
0.408 |
0.523 |
0.664 |
|
39 |
13.19 |
16.1 |
0.536 |
2.8 |
20 |
0.176 |
0.401 |
0.502 |
0.639 |
|
40 |
13.28 |
13.1 |
0.563 |
2.3 |
10 |
0.193 |
0.405 |
0.520 |
0.661 |
Figura. 1.
Resultados de convergencia del Pareto de los tres objetivos utilizados (CT, WRP, TAVE).
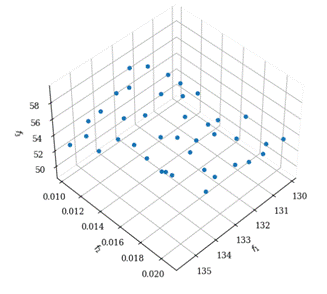
Utilizando la ecuación (19), se minimiza la relación entre los valores numéricos subjetivos y la normalización de los mismos. Este valor está representado por el parámetro COF, que aparece en la tabla 3. El costo de producción en el rango de CT = 13.0 $/pc, que permite realizar el proceso de rectificado con mejor acabado superficial 0.254 < TAVE < 2.54, aplicando la ecuación (4), el valor de la 0.47< Ra < 0.53; quedando dentro de los requerimientos mínimos establecidos al principio de la investigación, y que nos lleva a los mejores volúmenes de producción 10 < WRP < 20. Esto permite identificar las operaciones críticas en el proceso productivo, e identificar las mejores alternativas; para de esta manera aprovechar los materiales y lograr la calidad requerida en el acabado de las piezas.
El resultado de la optimización en relación a las variables subjetivas del modelo analizado en el proceso de rectificado y teniendo en cuenta la complejidad y dificultad de optimización para cada uno de los parámetros, mostró que la función objetivo combinada COF establece los valores en 0,398 < COF < 0,413. Se aprecia que tiene un nivel de importancia, pero con una pequeña diferencia de aproximación; considerando como variables de optimización para este estudio: velocidad de la muela abrasiva (Vs), la velocidad de la pieza (Vw), la profundidad de mecanizado (Doc) y el avance en profundidad (L). Para evaluar el desempeño del algoritmo NSGA-III sobre la rugosidad superficial del proceso de rectificado, para un mismo criterio, se comparan los resultados de esta investigación con los obtenidos aplicando otros métodos de análisis: Algoritmos Genéticos (GA) y Optimización por Enjambre de Partículas (PSO) (Tabla 4).
Tabla 4.
Comparación del resultado de la optimización de la rugosidad en el proceso de rectificado.
|
Método/Parámetros |
Vs |
Vw |
Doc |
L |
CT |
WRP |
Ra |
COF |
|
GA |
1.998 |
11.3 |
0.101 |
0.065 |
7.1 |
21.68 |
1.79 |
-0.187 |
|
PSO |
2.023 |
10 |
0.11 |
0.137 |
8.33 |
25.63 |
1.798 |
-0.224 |
|
NSGA-III |
2.289 |
14.5 |
0.16 |
0.01 |
13.3 |
14.82 |
0.5 |
0.41 |
Se observa en los resultados mostrados de los métodos GA y PSO superan la restricción de WRP >20 mm3/min N. El TC obtenido en NSGA-III es un 87,3 % superior al de GA y un 59,7 % superior al de PSO. Se cumplen los requisitos de Ra <= 1,8 µm y los valores límite de Doc y L.
De los resultados de las comparaciones, se concluye que el método NSGA-III propuesto como análisis multiobjetivo en el proceso de rectificado, para el acabado superficial, se puede conseguir en un entorno afín, variando los valores de los criterios de los métodos GA y PSO vistos.
CONCLUSIONES
Se demostró que el algoritmo de clasificación no dominado NSAG-III es una buena estrategia de optimización para plantas de producción, dadas las limitaciones en los valores recomendados de velocidad variable de la muela abrasiva (Vs), velocidad de la pieza de trabajo (Vw), profundidad de mecanizado (Doc) y avance en profundidad (L), durante el rectificado. Los valores óptimos se obtienen desarrollando un modelo de análisis multiobjetivo; se establecieron los objetivos seleccionados de mínimo coste de fabricación y acabado superficial y máxima productividad. Con base en los resultados obtenidos y las comparaciones, se concluye que, en la gestión del proceso de rectificado, el algoritmo propuesto es una solución favorable.
REFERENCIAS BIBLIOGRÁFICAS
Fu, G., Kapelan, Z., Kasprzyk, J. R., & Reed, P. (2013). Optimal design of water distribution systems using many-objective visual analytics. Journal of Water Resources Planning and Management, 139(6), 624-633. https://doi.org/doi:10.1061/(ASCE)WR.1943-5452.0000311
Huang, Y., Duan, H.-F., Zhao, M., Zhang, Q., Zhao, H., & Zhang, K. (2017). Probabilistic analysis and evaluation of nodal demand effect on transient analysis in urban water distribution systems. Journal of Water Resources Planning and Management, 143(8), 04017041. https://doi.org/doi:10.1061/(ASCE)WR.1943-5452.0000797
Kahhal, P., Brooghani, S. Y. A., & Azodi, H. D. (2013). Multi-objective optimization of sheet metal forming die using FEA coupled with RSM. Journal of Mechanical Science and Technology, 27(12), 3835-3842. https://doi.org/10.1007/s12206-013-0927-8
Patil, S. S., & Bhalerao, Y. J. (2019). Application of NSGA-II for optimisation of cylindrical plunge grinding process parameters. International Journal of Abrasive Technology, 9(4), 319-329. https://doi.org/10.1504/ijat.2019.106678
Sang, Y., & Tan, J. (2022). Intelligent factory many-objective distributed flexible job shop collaborative scheduling method. Computers & Industrial Engineering, 164, 107884. https://doi.org/https://doi.org/10.1016/j.cie.2021.107884
Xu, E. B., Yang, M. S., Li, Y., Gao, X. Q., Wang, Z. Y., & Ren, L. J. (2021). A multi-objective selective maintenance optimization method for series-parallel systems using NSGA-III and NSGA-II evolutionary algorithms. Advances in Production Engineering & Management, 16(3), 372-384. https://doi.org/https://doi.org/10.14743/apem2021.3.407
Wang, Y., Chen, C., Tao, Y., Wen, Z., Chen, B., & Zhang, H. (2019). A many-objective optimization of industrial environmental management using NSGA-III: A case of China’s iron and steel industry. Applied Energy, 242, 46-56. https://doi.org/https://doi.org/10.1016/j.apenergy.2019.03.048
Wang, J., Tian, Y., Hu, X., Li, Y., Zhang, K., & Liu, Y. (2021). Predictive modelling and Pareto optimization for energy efficient grinding based on aANN-embedded NSGA II algorithm. Journal of Cleaner Production, 327, 129479. https://doi.org/https://doi.org/10.1016/j.jclepro.2021.129479
Zhang G., Liu M., Li J., Ming W. , Shao X. & Huang Y. (2014). Multi-objetive optimization for surface grinding process using a hybrid particle sward optimization algorithm. International Journal Advanced Manufacturing Technology, 71, 1861-1872. https://doi.org/https://doi.org/10.1007/s00170-013-5571-z
Nomenclatura:
|
Símbolo |
Descripción |
Símbolo |
Descripción |
|
Mc |
Costo por hora |
Nt |
Tamaño de la pieza |
|
P |
Número de piezas |
Ntd |
Numero total de piezas que pueden ser rectificado durante la vida de cubierta |
|
Lw |
Longitud de la pieza |
Cd |
Costo de cubierta |
|
Lc |
Longitud limpia rectificada |
Cs |
Costo de la rueda por mm3 |
|
fb |
Volumen de profundidad transversal |
CT* |
Limite de costo de la producción. |
|
aw |
Total grosor de corte |
Rc |
Dureza de la Pieza |
|
ap |
Avance profundidad de rectificado |
Ra* |
Límite del acabado de la pieza durante el rectificado |
|
Sp |
Número de pizcas en el rectificado |
VOL |
Porciento de aderencia a la rueda |
|
De |
Diámetro de la rueda |
dg |
Tamaño del grano |
|
bs |
Ancho de la rueda |
WRP* |
Límite de material removido de la pieza |
|
G |
Radio de rectificado |
Km |
Rigidez estatica de la maquina herramienta |
|
Sd |
Distancia de la rueda parada |
Rem |
Características dinámicas de la máquina herramienta |
|
Vr |
Velocidad de la rueda parada |
A0 |
Porciento inicial de desgaste |
|
t1 |
Tiempo de carga y descarga de la pieza |
Ku |
Constante de desgaste |
|
tch |
Tiempo de ajuste de la máquina herramienta |
Ka |
Constante dependiente de refrigeración y tipo de grano de la rueda. |
|
Nd |
Número total de piezas que pueden ser ground entre dos dressings |
Vs |
Velocidad de la rueda. |
|
Vw |
Velocidad de la pieza |
Doc |
Profundidad de corte |
|
L |
Avance |
Ra |
Rugosidad superficial |