Optimización multiobjetivo mediante algoritmos evolutivos, para el diseño de desalinizadores solares de humidificación deshumidificación
Geosvanis Boligán Rojas
Centro de Estudios CAD/CAM, Universidad de Holguín, Cuba. Universidad de Holguín, Campus “Oscar Lucero Moya”.
ORCID: 0000-0001-9892-6968
geosvanisbr@uho.edu.cu
Carlos Trinchet Varela
Centro de Estudios CAD/CAM, Universidad de Holguín, Cuba. Universidad de Holguín, Campus “Oscar Lucero Moya”. ORCID: 0000-0001-5375-2968
carlos.trinchet@uho.edu.cu
Roberto Pérez Rodríguez
Centro de Estudios CAD/CAM, Universidad de Holguín, Cuba. Universidad de Holguín, Campus “Oscar Lucero Moya”.
ORCID: 0000-0001-5741-5168
roberto.perez@uho.edu.cu
RESUMEN
Los desalinizadores solares con el ciclo de humidificación deshumidificación (DSCHDH) son una opción viable para suplir el problema de escasez de agua potable en zonas cercanas a las costas de poca demanda y lejos de los sistemas de abasto tradicionales. Esta investigación tiene el propósito de proponer una metodología de diseño mejorada de DSCHDH. El objetivo propuesto, resulta en desarrollar un método que asegura el diseño adecuado mediante el empleo de los sistemas diseño asistido por computadora / análisis de ingeniería asistido por computadora (CAD/CAE) y la Inteligencia Artificial. Se configura una optimización multiobjetivo mediante algoritmos evolutivos que brindan un conjunto de soluciones eficientes y más económicas. Esto se desarrolla obteniendo del proceso de optimización multiobjetivo los valores termodinámicos óptimos y las dimensiones geométricas correspondientes a estos las cuales se enlazan a un sistema CAD capaz de representar el sistema y que soporta análisis de ingeniería, o sea, un sistema CAD/CAE. El aporte de la investigación se deriva del planteamiento del estudio de este tipo de sistemas en este marco.
Palabras clave: optimización, multiobjetivo, CAD, CAE, desalinización.
Multi-objective optimization using evolutionary algorithms, for the design of solar humidification dehumidification desalinators
ABSTRACT
Solar desalination systems with the humidification-dehumidification cycle (DSCHDH) are a viable option to solve the problem of scarcity of drinking water in places near the coast with little demand and far from traditional supply systems. This research has the purpose of proposing an improved design methodology of DSCHDH. The proposed objective is to develop a method that ensures adequate design through the use of computer-aided design / computer-aided engineering analysis (CAD/CAE) systems and Artificial Intelligence. A multi-objective optimization is configured using evolutionary algorithms that provide a set of efficient and cheaper solutions. This is developed by obtaining from the multi-objective optimization process the optimal thermodynamic values and the geometric dimensions corresponding to these, which are linked to a CAD system capable of representing the system and supporting engineering analysis, that is, a CAD/CAE system. The contribution of the research derives from the approach of the study of this type of systems in this framework.
Keywords: optimization, multi-objective, CAD, CAE, desalinization.
INTRODUCCIÓN
La demanda de agua ya supera la oferta en muchas partes del mundo y, a medida que la población mundial continúa aumentando, también lo hace la demanda de agua. Se espera que para 2025, más del 60% de la población mundial tenga escasez de agua. En cuanto al hecho de que el agua de mar es una de las fuentes de agua más convenientes, la desalinización puede ser una solución práctica a esta preocupación.
Los DSCHDH, son una opción viable para abastecer de agua potable zonas apartadas de poca demanda y cercanas a las costas, donde los sistemas tradicionales como de ósmosis inversa (OI), multietapas de evaporación súbita (MES), evaporación multi efecto (EME) y vapor compresión (VC) resultan poco factibles. Igualmente, el hecho de ser el DSCHDH un método que trabaja a bajas temperaturas le da ventajas para poder ser aplicado con energía solar y casi como la única opción en casos de agua con alta salinidad.
Figura 1.
Esquema de un DSCHDH
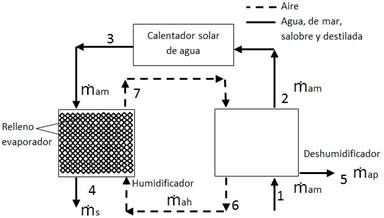
La figura 1 muestra un DSCHDH
de circulación cerrada de aire y circulación abierta de agua; los números en la
misma representan las entradas y salidas de cada etapa del sistema tanto para
el aire como para el agua y se usan como subíndices en las ecuaciones, cada uno
representa un valor de temperatura t (0C). El calor se introduce en
el sistema mediante un calentador solar de agua (CSA), antes del humidificador;
igualmente, en la referida figura se observa la ubicación del relleno
evaporador en el humidificador. Donde, 
(kg/s) es el caudal
másico, 
caudal másico del
agua de mar, 
caudal másico del aire
húmedo, 
caudal másico del agua
de gran concentración de sales y 
el caudal másico del
agua potable que sale destilada del deshumidificador.
En la figura 1, puede verse el agua de mar entrar al deshumidificador 1, sirviendo de agente de enfriamiento en el condensador, sale con mayor temperatura 2 y es calentada aún más en el CSA, el agua de mar ya con mayor temperatura 3, entra al humidificador donde luego de ser asperjada cae en el relleno evaporador donde ocurre la evaporación de parte de la misma en un proceso donde pierde calor al entregarle al aire parte de su masa evaporada, saliendo 4 con mayor concentración de sales. El ciclo cerrado del aire se observa al entrar al humidificador 6 (el número 6 coincide para la entrada del humidificador y salida del deshumidificador, pues conserva igual características de humedad y temperatura), en el humidificador se carga de agua que toma de la evaporación del agua de mar. Sale del humidificador para entrar al deshumidificador 7 y al enfriarse aporta el agua potable 5. Realmente el agua que sale por 5, en la figura descrita, es un agua destilada se puede considerar potable si va directamente a un uso agrícola, para consumo humano llevaría otro tratamiento en procesos mucho más sencillos comparados con el proceso de destilación en sí; realmente en la mayoría de las referencias sobre el tema se le dice agua potable.
La existencia de una adecuada metodología de diseño de estos sistemas, permitiría su mejora junto con su mejor utilidad práctica, lo cual puede ser potenciado con métodos de inteligencia artificial. Se observa que a pesar de las ventajas del uso de la optimización multiobjetivo mediante algún método de inteligencia artificial, hay pocos ejemplos para optimizar solo un parámetro a la vez y muy pocas referencia de optimización multiobjetivo de los DSCHDH. Entre los métodos más usados se encuentra el de algoritmos genéticos (AG) muy usado en la optimización multiobjetivo.
Los algoritmos evolutivos multiobjetivo (AEMO) han sido utilizados previamente para operar investigaciones sobre DSCHDH (Farid & Al-Hajaj, 1996), en cuyos textos se refleja la evolución de los mismos y su principio de funcionamiento (Bundschuh, Kaczmarczyk, Ghaffour, & Tomaszewska, 2021; Kasaeian et al., 2019; Lienhard V, 2019; Mohamed, Ahmed, & Shahdy, 2020). Sobre tratamiento más específico del diseño de los DSCHDH se puede consultar (Ettouney, 2005; Narayan, John, Zubair, & Lienhard, 2013; Sharqawy, Antar, Zubair, & Elbashir, 2014), los cuales sin embargo no aprovechan las grandes posibilidades de las metodologías de diseño hasta llegar al uso de técnicas CAD/CAE y similares; de lo cual se referencia en (Boligan Rojas, Avila Rondon, & Melendez Gurrola, 2018; Finger & Dixon, 1989a, 1989b; Jaluria, 2008; Li et al., 2004; Pahl & Beitz, 1998; Salomons, van Houten, & Kals, 1993; Tseng, Wang, & Shih, 2007). A partir de lo anterior se deduce la importancia del desarrollo de metodologías de diseño para mejoras de los DSCHDH. Referido a la optimización de objetivos simples puede citarse a (Mistry, Mitsos, & Lienhard V, 2011; Zamen, Amidpourb, & Soufari, 2009) y muy importante (Soufari, Zamen, & Amidpour, 2009). Ya en cuanto a referencias de optimización multiobjetivo por métodos evolutivos de DSCHDH se tiene a (Khedmati & Shafii, 2020; Rafigh, Mirzaeian, Najafi, Rinaldi, & Marchesi, 2017) y otras referencias de sistemas similares que pueden servir para la comprensión del método como (Zhang, Zhang, Zheng, You, & Wang, 2019) y (Zhou, 2021). El algoritmo NSGA-II fue desarrollado por Kalyanmoy Deb y colaboradores cuyas referencias recomendadas son (Deb, 2000a, 2000b, 2001a, 2001b, 2001c, 2002).
Seguidamente se muestra resumido las principales funciones objetivos usadas previamente relacionadas de una forma u otra con este marco investigativo.
Tabla 1:
Funciones objetivos usadas en referencias previas, relacionadas con el marco investigativo del presente trabajo.
|
Autor (es) |
Funciones Objetivo |
|
Zamen et al., 2009 |
Min(Capp) |
|
Soufari et al., 2009 |
Min(ETS-C) |
|
|
Max(Prod) |
|
|
Max(GOR) |
|
Mistry et al., 2011 |
Max(GOR) |
|
Rafigh et al., 2017 |
Min(ETS-C) |
|
Min(A-HD/AP-P) |
|
|
Sayyaadi y Ghorbani, 2018 * |
Min(Capp) |
|
Max(AP-P) |
|
|
Zhang et al. 2019 |
Max(AP-P) |
|
|
Max(GOR) |
|
|
Min(Capp) |
|
Khedmati et al., 2020 |
Min(VS) |
|
|
Max(GOR) |
|
Kolahi el al., 2020 * |
Max(AP-P) |
Figura 2
Funciones objetivo estudiados por diversos autores.
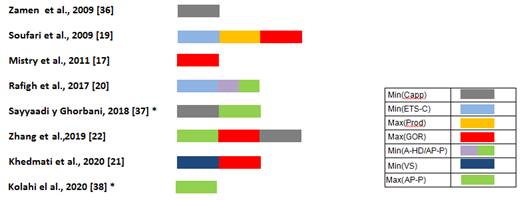
La figura 2, es una representación gráfica de la tabla 1. Las abreviaturas empleadas se explican a continuación.
AP-P: Agua potable producida (kg/s)
Capp: Costo producción de AP-P ($)
ETS-C: Energía térmica específica consumida (kJ/s)
A-HD: Área del humidificador + Área del Deshumidificador (m2)
VS: Volumen del sistema (m3)
GOR: Relación de ganancia a la salida (-)
Prod: Productividad (-)
AM-A: Agua de mar alimentada al sistema (kg/s)
Max y Min, maximizar y minimizar la función respectiva. El asterisco (*) significa que la referencia tiene otras funciones objetivos de otras partes del sistema. Max y Min, maximizar y minimizar la función respectiva. El asterisco (*) significa que la referencia tiene otras funciones objetivos de otras partes del sistema.
METODOLOGÍA
Con lo analizado hasta aquí, se tiene la situación problémica, de requerir mejores diseños de DSCHDH, a ser usados en lugares apartados de poco consumo del agua que escasea. La literatura sobre el tema modela matemáticamente este tipo de sistemas, revelando la influencia de muchos factores dependientes los unos de los otros en el funcionamiento de los DSCHDH, que deberían tenerse en cuenta en su diseño. Igualmente varias referencias reflejan optimizaciones de parámetros simples, sin embargo, ello implica un análisis incompleto pues la mejora de un factor implica empeorar otro. La optimización multiobjetivo basada en técnicas evolutivas es una meta heurística surgida para resolver este tipo de problemas, las cuales no están suficientemente desarrolladas para DSCHDH, se requieren nuevas propuestas de algoritmos con al menos 3 funciones objetivos y estar basadas en modelos matemáticos más avanzados, por la referida influencia mutua multi - factores.
Por tanto el presente trabajo tiene como objetivo, obtener un método mejorado de optimización multiobjetivo mediante algoritmo NSGA-II en el proceso de diseño de DSCHDH, que permitan generar configuraciones más económicas de los mismos con mejor eficiencia de funcionamiento.
Por
tanto, luego de un exhaustivo análisis aplicando métodos histórico lógico
inductivos, se propone una metodología de optimización multiobjetivo mediante
algoritmo NSGA-II, de los parámetros de diseño 
, 
, temperatura mínima
del sistema a la entrada del deshumidificador y temperatura máxima a la
entrada del humidificador del agua a procesar respectivamente, 
temperatura del agua a
procesar a la salida del humidificador, 
, la temperatura del
agua a procesar a la salida del deshumidificador, mientras que, 
, 
, 
, 
son la temperatura y
humedad relativa del aire a la salida del humidificador y el deshumidificador
respectivamente, la temperatura en 0C y la humedad relativa
adimensional (-), que aseguren las mejores soluciones en sus parámetros
funcionales, los cuales son, costo del sistema, relación de productividad de
agua potable respecto a agua alimentada al sistema y la relación de ganancia a
la salida o GOR que da cuentas del calor del proceso que es reincorporado al
sistema. Los parámetros de diseño se emplean para calcular los valores de
efectividad según corresponda que determinan las restricciones, también son
parte de las ecuaciones de cálculo de los valores geométricos de las partes
activas del sistema. Ello configura una optimización multiobjetivo mediante
algoritmos evolutivos que brindan un conjunto de soluciones eficientes y más
económicas.
Tabla 2:
Parámetros de diseño y sus rangos.
|
Parámetros de diseño |
Valor mínimo |
Valor máximo |
|
|
23 |
30 |
|
|
40 |
70 |
|
|
37 |
55 |
|
|
27 |
35 |
|
|
27 |
35 |
|
|
25 |
35 |
|
|
0.7 |
1 |
|
|
0.7 |
1 |
Tabla 3:
Rango de los datos de entrada.
|
Datos de entrada |
Valor mínimo |
Valor máximo |
|
AM-A (kg/s) |
0.05 |
0.3 |
|
|
33 |
50 |
|
|
101.325 |
101.325 |
|
|
1.5 |
1.5 |
|
|
5 |
100 |
Se propone, basado en el algoritmo NSGA-II: Min(A-HD), Min(AM-A /AP-P) y Min(1/ GOR),
Sujeto a:
(1)
(2)
Donde
son la efectividad del
humidificador y del deshumidificador respectivamente (-).
(3)
(4)
(5)
(6)
(7)
Donde 
(W) es el calor que
sale (ou) y entra (in) al sistema, mientras que 
(W/K) es la entropía
generada por el sistema a la entrada y la salida. Los sufijos “hu” y “de”
indican humidificador y deshumidificador respectivamente. El término 
es un valor a
seleccionar en el rango de 10-9 – 0.01, en dependencia de la
exactitud que requieren los resultados, que para casos de problemas de
ingeniería 0.01 sirve perfectamente. Las ecuaciones (1-6) se basan en la
referencia (Narayan, Sharqawy, Lienhard V, & Zubair, 2010), donde se
explica el término de diferencia de temperaturas extremas (
) y temperatura de (del
inglés pinch) “pellizco” (
) ambas en 0C.
Los parámetros de optimización y sus cotas se enumeran en
las tablas 2 y 3.
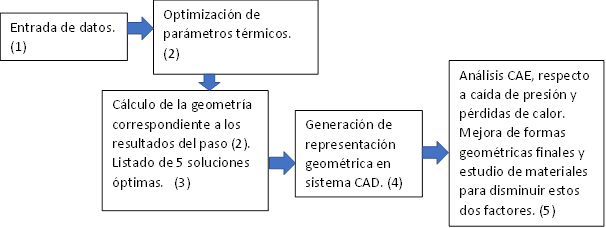
Figura 3
Esquema general de la metodología propuesta.
.
RESULTADOS Y DISCUSION
La figura 3, muestra el esquema general de la metodología propuesta; se puede comentar el hecho de que se presentan dos pasos separados, primero se obtienen los valores térmicos y luego se calcula la geometría correspondiente para generar el listado de soluciones óptimas, ello se debe a que se observa en las pruebas realizadas hasta el momento, necesidad de manejar la carga de procesamiento. El cálculo de la geometría del humidificador es a partir de las variables térmicas y requieren la ejecución del cálculo de ecuaciones diferenciales mediante el método de Runge–Kutta de cuarto orden (Kloppers & Krӧger, 2005) y del deshumidificador mediante la combinación de ecuaciones dadas en la referencia (Triboix, 2009) y se complementa con (Sharqawy et al., 2014), al menos el cálculo del humidificador requiere un importante consume de recursos de cálculo, por eso debe separarse como se indica en la figura 3 en los pasos (3) y (4). Sobre el paso (5) de la figura 3, se comenta que refleja una de las ventajas del presente enfoque; existen formas de cálculo de las pérdidas de presión y de calor, sin embargo implementarlo de esta forma, brinda la ventaja de poder establecer correcciones ya sobre el plano geométrico del sistema obtenido.
Las ecuaciones (1-6) son basadas en la referencia (Narayan et al., 2010) como ya se mencionó, en ese mismo trabajo se puede profundizar sobre las formas de cálculo de este tipo de sistemas buscando la mayor eficiencia posible, cuestión que ha tributado a la presente propuesta. Las ecuaciones termo físicas del agua y el aire se basan en las referencias (Nayar, Sharqawy, Banchik, & Lienhard V, 2016; Nayar, Sharqawy, & Lienhard V, 2016; Perez Galindo, Payan Rodriguez, & Martin Dominguez, 2007; Sharqawy, Lienhard V, & Zubair, 2010). El estudio de resultados previos contribuye a los valores de las tablas 2 y 3.
El
estudio mediante métodos histórico lógicos inductivos, ha dado como resultado
el método planteado en el epígrafe de resultados. Debe resaltarse que aquí ya
se reflejan análisis basados en las ecuaciones (4) y (6), lo cual se refleja en
los rangos de temperaturas de la tabla 2, o sea, una diferencia muy pequeña de
las 
del humidificador
puede dar valores adecuados incluso óptimos del resto de las ecuaciones pero no
cumplir las ecuaciones (4) y (6) lo cual físicamente es imposible, por tanto
tener una metodología que lo tenga en cuenta significa valores más cercanos a la
realidad; una reflexión similar se aplica incluyendo el deshumidificador, pues 
muy pequeñas
significarían dimensiones grandes del sistema y por ende afecta el costo contra
producción, aunque esto se decanta por la propia optimización, contrario a lo
explicado para el humidificador respecto a las ecuaciones (4) y (6), por lo que
resulta necesaria la ecuación (7); se recomienda profundizar sobre este tema
consultando (Mistry et al., 2011; Narayan et al., 2010; Rafigh et al., 2017).
Otra cuestión a tener en cuenta en valorar los resultados obtenidos, estriba alrededor del paso (5) de la figura 3. Ya se comentó en el epígrafe de los resultados que este análisis se puede hacer mediante ecuaciones introducidas en la propia optimización, sin embargo se prefiere hacer hincapié en el análisis termodinámico obviando estos factores y su enlace con las dimensiones del sistema; realizarlo mediante un sistema CAD/CAE más en un ambiente con objetivos de ingeniería y diseño, aporta la automatización de la representación geométrica y del análisis de las caídas de presión y pérdidas de calor se puede combinar con rectificaciones de formas en el plano del sistema, igual se puede incluir análisis comparativos y de validación de resultados del resto de los parámetros.
CONCLUSIONES
El objetivo de proponer un método de diseño mediante la combinación de optimización multiobjetivo mediante algoritmo NSGA-II para tributar a sistema CAD/CAE, ha sido cumplido. Con este trabajo se puede contar con un punto de partida para implementar mejoras a los DSCHDH. Igualmente sirve de punto de partida para futuras investigaciones.
REFERENCIAS BIBLIOGRÁFICAS
Boligan Rojas, Geosvanis, Avila Rondon, Ricardo L., & Melendez Gurrola, Ana C. (2018). Mechanical Engineering Design Theory Framework for Solar Desalination rocesses: A Review and Meta - Analysis. Iranian Journal of Energy and Environment, 9(2), 137-145. doi: http://10.5829/ijee.2018.09.02.09
Ettouney, H. (2005). Design and analysis of humidification dehumidification desalination process. Desalination, 183(1-3), 341-352. doi: http://dx.doi.org/10.1016/j.desal.2005.03.039
Farid, M. M., & Al-Hajaj, A.W. (1996). Solar desalination with a humidification-dehumidification cycle. Desalination, 106(1-3), 427-429. doi: http://dx.doi.org/10.1016/S0011-9164(96)00141-5
Kloppers, Johannes C., & Krӧger, Detlev G. (2005). A critical investigation into the heat and mass transfer analysis of counterflow wet-cooling towers. International Journal of Heat and Mass Transfer, 48(3-5), 765–777. doi: https://doi.org/10.1016/j.ijheatmasstransfer.2004.09.004
Pahl, G., & Beitz, W. (1998). Engineering Design A Systematic Approach: Springer.
Perez Galindo, Jose A., Payan Rodriguez, Luis A., & Martin Dominguez, Ignacio R. (2007). LB-07-047: Thermodynamic Properties for Saturated Air, an Engineering Correlation. ASHRAE Transactions, 113(2), 449-456. doi: https://www.techstreet.com/standards/lb-07-047-thermodynamic-properties-for-saturated-air-an-engineering-correlation?product_id=1712682
Zhou, Shihe. (2021). Parametric study and multi-objective optimization of a combined cooling, desalination and power system. Desalination and Water Treatment. doi: https://doi.org/10.5004/dwt.2021.26994